Madison Math Circle
What is it?
The UW-Madison math department organizes a series of talks aimed at interested middle school and high school students throughout the semester. Our goal is to present fun talks that give students a taste of interesting ideas in math and science. In the past we've had talks about plasma and weather in outer space, the way images are shaded in video games, and how credit card numbers are securely transmitted over the internet.
Important: After each talk we'll have pizza provided by the department, and students will have an opportunity to mingle and chat with the speaker to ask questions about college, careers in science, etc.
Alright, I want to come!
Great! If you're a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in Van Vleck Hall on the UW campus). We'd also appreciate if you email us the dates that your group will be attending, so we can purchase the appropriate amount of pizza.
If you're a student, speak with your high school teacher about organizing a car pool to the math night (and tell us how many people are coming!)
Questions?
If you have any questions, suggestions for topics, or so on, just email the organizers: math-night@math.wisc.edu.
Talks this semester
More details about each talk to follow. All talks are at 7pm in Van Vleck Hall B231.
| Date | Speaker | Talk (click for more info) |
|---|---|---|
| October 3rd, 2011 | Prof. Gheorghe Craciun | Introduction to Mathematical Proofs |
| October 10th, 2011 | Prof. Gheorghe Craciun | Introduction to Mathematical Proofs (part 2) |
| TBA | Prof. Bret Larget | TBA |
| TBA | Prof. Sigurd Angenant | TBA |
| TBA | Prof. Jean-Luc Thiffeault | TBA |
Introduction to Mathematical Proofs
October 3rd, 2011
Introduction to Mathematical Proofs
The first ever meeting of the Madison Math Circle will describe mathematical proofs using many examples from 2D and 3D geometry, algebra, logic, puzzles, and games (yes, games!). Free and open to the public. Middle school and high school students are invited to attend.
Speaker: Andrew Bridy
Andrew is a third year math Ph. D. student studying algebra and computer science. Before coming to graduate school, he taught high school math for a year and was deployed with the Peace Corps to Honduras. Andrew is an avid video game fan - you should ask him to tell you about his favorite PC video games of the late 1990's.
The 0.5th Dimension
March 10th, 2011
A Harrowing Journey to the 0.5th Dimension
We frequently think about two dimensional spaces, like a map of a country, or three dimensional spaces, like the Holodeck from Star Trek. But what exactly is "dimension", anyway? This turns out to be a surprisingly deep question, without a unique answer. But asking it is still useful, and leads us to the strange and beautiful notion of Hassdorf dimension, one of the fndamentals of fractal geometry, which gives a meaning to non-integer dimensions. We will discuss Haussdorf dimension and its motivation, and see an application to psychology.
Speaker: Ed Dewey
Ed is a first year Ph. D. student in mathematics. He used to be in a ska band.
Cutting & Pasting
March 24th, 2011
The Bolyai-Gerwein theorem says that any two polygons of the same area have an "equi-dissection". In other words, there is a way to cut up one of the polygons into pieces (using straight line cuts) that can be rearranged to form the other. This deep theorem is surprisingly recent compared to much of classical geometry and has many interesting generalizations. During this weeks talk we will prove the theorem as a group using little more then argument by "scissors and glue."
Here are some fun applets to see this in action:
http://demonstrations.wolfram.com/AnExampleOfTheBolyaiGerwienTheorem/
http://www.cut-the-knot.org/Curriculum/Geometry/TwoRectangles.shtml
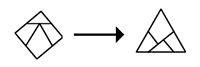
An example of dissecting a square into pieces that form a triangle of the same area.
Speaker: Lalit Jain
Lalit is a first year Ph. D. student in mathematics interested in number theory and computer science. Before coming to graduate school, Lalit was a high school math teacher with Teach For America in San Francisco. You should ask Lalit about who shot Frances in the video game Left 4 Dead.
Tilings
April 7th, 2011
Tilings
Tilings in the mathematical sense mean non-overlapping, gap-free coverings of the plane by certain shapes. For instance, one can take (infinitely many) squares and place them on the infinite plane as they are on a chessboard, nicely fitting next to each other. This is maybe the simplest example. But if one takes regular pentagons, it is impossible to form a tiling using only them.
The first class of interesting tilings we will discuss are the Penrose tilings. These involve two different shapes, the "kite" and the "dart". Not only it is fun to play with them and to try to make different arrangements, but these tilings have really interesting mathematical properties. Just to mention one of these: the ratio of the number of kites and darts - which I'll make precise - in all the possible arrangements is always the same, and it is the golden ratio!
Tilings have an artistic nature as well. The Dutch graphic artist M. C. Escher is famous for his math-connected drawings, and in fact many of these are tilings with funny shapes, birds for example. Another series of masterpieces by him are the woodcuts Circle Limit I-IV which picture hyperbolic tilings of the disk using funny graphics again. We will talk about their mathematical background, and also about how to write a program that makes a hyperbolic tiling out of an arbitrary image file.
Speaker: Balazs Strenner
Balazs is a first year PhD student originally from Hungary, land of many fantastic mathematicians and scientists. Balazs is quite merciless as the Deputy Sheriff in the card game Bang!
Face Recognition
April 28th, 2011
Invariant-Based Face Recognition
I shall describe the main difficulties with automated face recognition and how our team of mathematicians, engineers, and computer scientists overcame some of them by using mathematical invariants.
What are invariants? Invariants are features that do not change under 3D rotation and translation. An example is the curvatures at the tip of the nose. These curvatures do not change, regardless of what angle you look at the face from. The problem though in practice is that curvatures are very sensitive to small changes in the measurements used to compute them, so that simply rounding of the measurements can lead to very different, not invariant numbers.
For this reason, invariants have been rejected in the past for recognizing faces because they were not robust to measurement error, and so we decided to come up with a new family of robust invariants. I shall report how our implementation of this won us 2nd place in the 3D section of the national Face Recognition Grand Challenge.
Speaker: Professor Nigel Boston
Nigel Boston is a Professor in the Departments of Mathematics and Electrical & Computer Engineering at UW-Madison. Nigel works in many interesting areas, including applying research from algebra and number theory to real world problems in engineering.