Madison Math Circle: Difference between revisions
Ksrivastava4 (talk | contribs) No edit summary |
|||
| (74 intermediate revisions by 6 users not shown) | |||
| Line 2: | Line 2: | ||
For the site in Spanish, visit [[Math Circle de Madison]] | For the site in Spanish, visit [[Math Circle de Madison]] | ||
=What is a Math Circle?= | =What is a Math Circle?= | ||
The Madison Math Circle is a weekly series of mathematically based activities aimed at interested middle school and high school students. It is an outreach program organized by the UW Math Department. Our goal is to provide a taste of exciting ideas in math and science. In the past we've had talks about plasma and weather in outer space, video game graphics, and encryption. In the sessions, students (and parents) are often asked to explore problems on their own, with the presenter facilitating a discussion. The talks are independent of one another, so new students are welcome at any point. | The Madison Math Circle is a weekly series of mathematically based activities aimed at interested middle school and high school students. It is an outreach program organized by the UW Math Department. Our goal is to provide a taste of exciting ideas in math and science. In the past we've had talks about plasma and weather in outer space, video game graphics, and encryption. In the sessions, students (and parents) are often asked to explore problems on their own, with the presenter facilitating a discussion. The talks are independent of one another, so new students are welcome at any point. | ||
| Line 22: | Line 17: | ||
=All right, I want to come!= | =All right, I want to come!= | ||
Our in person talks will be at, <b>Monday at 6pm in 3255 Helen C White Library</b>, during the school year | Our in person talks will be at, <b>Monday at 6pm in 3255 Helen C White Library</b>, during the school year. New students are welcome at any point! There is no fee and the talks are independent of one another. You can just show up any week, but we ask all participants to take a moment to register by following the link below: | ||
[https:// | [https://forms.gle/5QRTkHngWf43nmCC9 '''Math Circle Registration Form'''] | ||
All of your information is kept private, and is only used by the Madison Math Circle organizer to help run the Circle. | All of your information is kept private, and is only used by the Madison Math Circle organizer to help run the Circle. | ||
If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus. If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in 3255 Helen C White Library, on the UW-Madison campus, right next to the Memorial Union). | If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus. If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in 3255 Helen C White Library, on the UW-Madison campus, right next to the Memorial Union). | ||
== Fall Schedule == | |||
<center> | <center> | ||
{| style="color:black; font-size:120%" border="1" cellpadding="14" cellspacing="0" | {| style="color:black; font-size:120%" border="1" cellpadding="14" cellspacing="0" | ||
|- | |- | ||
! colspan="4" style="background: #e8b2b2;" align="center" | | ! colspan="4" style="background: #e8b2b2;" align="center" | Fall Schedule | ||
|- | |||
! Date !! Location and Room || Speaker || Title | |||
|- | |||
| Oct 7 || 3255 College Library || Caitlin Davis || How to Cut a Cake (Fairly) | |||
|- | |||
| Oct 14 || 3255 College Library || Uri Andrews || Math, Philosophy, Psychology, and Artificial Intelligence | |||
|- | |||
| Oct 21 || 3255 College Library || Sam Craig || Fractal geometry and the problem of measuring coastlines | |||
|- | |||
| Oct 28 || 3255 College Library || Cancelled || Cancelled | |||
|- | |||
| Nov 4 || 3255 College Library || Sam Craig || Proofs of the Pythagorean theorem, new and old. | |||
|- | |||
| Nov 11 || 3255 College Library || Chenxi Wu || Heron’s method for approximating square roots | |||
|- | |- | ||
| Nov 18 || 3255 College Library || Diego Rojas || Non-Transitive Dice: The Math That Doesn’t Play Fair | |||
|- | |- | ||
| | | Nov 25 || 3255 College Library || Kaiyi Huang || A geometric investigation into a space shuttle failure | ||
|- | |- | ||
| | | Dec 2 || 3255 College Library || TBA || TBA | ||
|- | |- | ||
| | | Dec 9 || 3255 College Library || TBA || TBA | ||
|- | |- | ||
| | | Dec 16 || 3255 College Library || TBA || TBA | ||
|- | |- | ||
|} | |} | ||
</center> | </center> | ||
= Fall Abstracts = | |||
=== Abstract 10/7 === | |||
== | |||
<center> | <center> | ||
{| style="color:black; font-size:100%" table border="2" cellpadding="10" width="700" cellspacing="20" | |||
{| style="color:black; font-size: | |||
|- | |- | ||
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Caitlin Davis''' | |||
|- | |- | ||
| bgcolor="#BDBDBD" align="center" | '''Title: How to Cut a Cake (Fairly)''' | |||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
Imagine you and a friend are sharing a cupcake. How can you cut the cupcake so that each of you gets your fair share? If you've ever shared a cupcake (or some other treat) with a friend, you might have an answer! Now what if you're sharing a cake with several friends? Can we use the same strategy to cut the cake fairly? We'll talk about how math can be used to study questions like this. | |||
|} | |||
</center> | |||
=== Abstract 10/14 === | |||
<center> | |||
{| style="color:black; font-size:100%" table border="2" cellpadding="10" width="700" cellspacing="20" | |||
|- | |||
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Uri Andrews''' | |||
|- | |||
| bgcolor="#BDBDBD" align="center" | '''Title: Math, Philosophy, Psychology, and Artificial Intelligence''' | |||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
People come to understand the truth via a process of arguing. This could be a philosophical debate. This could be an internal dialogue. This could be in a courtroom. This could be deciding with your family where to go for dinner. These are all different forms of argumentation, with different rules for when you are convinced. In a courtroom, you have to be convinced beyond a reasonable doubt, whereas when deciding where to go for dinner, you might just have to look hungriest to win. These processes can be mathematically modeled. Moreover, this is important for the modern goal of teaching a computer how to think and how to understand human reasoning (Artificial Intelligence). | |||
|} | |||
</center> | |||
=== Abstract 10/21 === | |||
<center> | |||
{| style="color:black; font-size:100%" table border="2" cellpadding="10" width="700" cellspacing="20" | |||
|- | |- | ||
| | | bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Sam Craig''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" align="center" | '''Title: Fractal geometry and the problem of measuring coastlines''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
A fractal is a shape which looks about the same when you look closely as when you look far away. I will show some examples of fractals that arise in math (like the Sierpinski triangle) and in nature (like the coastline of an island) and discuss the difficulties in determining what the length of a fractal means. | |||
|} | |||
</center> | |||
=== Abstract 11/4 === | |||
<center> | |||
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table | |||
|- | |||
|- | |- | ||
| | | bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Sam Craig''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" align="center" | '''Title: Proofs of the Pythagorean theorem, new and old.''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
The Pythagorean theorem has been known for thousands of years and over that time, people have found a number of different ways to prove the theorem. We will talk about a proof given by Pythagoras, a proof by US President Andrew Garfield, and a very recent proof (that you might have heard of in the news) by Calcea Johnson and Ne'Kiya Jackson. | |||
|} | |} | ||
</center> | </center> | ||
== | === Abstract 11/11 === | ||
<center> | <center> | ||
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table | |||
{| style="color:black; font-size: | |||
|- | |- | ||
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Chenxi Wu''' | |||
|- | |- | ||
| bgcolor="#BDBDBD" align="center" | '''Title:Heron’s method for approximating square roots.''' | |||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
We will talk about Heron's method for approximating square roots. This will lead us on a journey through approximation methods including Newton's method, through algebraic concepts like the p-adic numbers, and Hensel's Lemma. | |||
|} | |||
</center> | |||
=== Abstract 11/18 === | |||
<center> | |||
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table | |||
|- | |- | ||
| | | bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Diego Rojas''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" align="center" | '''Title:Non-Transitive Dice: The Math That Doesn’t Play Fair.''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
What if I told you there’s a set of dice where winning doesn’t follow the rules you expect? In this talk, we’ll explore the strange and surprising world of non-transitive dice, where the usual logic of “if A is better than B, and B is better than C, then A must be better than C” simply falls apart. Using math, probability, and a little imagination, we’ll uncover why these dice defy intuition and how they challenge our understanding of competition and strategy. Get ready to think about games—and math—in a whole new way! | |||
|} | |||
</center> | |||
In this | |||
| | |||
=== Abstract 11/25 === | |||
<center> | |||
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table | |||
|- | |- | ||
| | | bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Kaiyi Huang''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" align="center" | '''Title:A geometric investigation into a space shuttle failure''' | ||
|- | |- | ||
| | | bgcolor="#BDBDBD" | | ||
We know that a circle has the same width in every direction, but is it the only object that has this property? NASA engineers assumed so, which, together with a string of other mistakes, might have led to the tragic failure of their space shuttle launch. Let’s look further into this problem so that we won’t make the same mistake again! | |||
|} | |} | ||
</center> | </center> | ||
| Line 198: | Line 180: | ||
The Madison Math Circle is organized by a group of professors and graduate students from the [http://www.math.wisc.edu Department of Mathematics] at the UW-Madison. If you have any questions, suggestions for topics, or so on, just email the '''organizers''' [mailto:mathcircleorganizers@g-groups.wisc.edu here]. We are always interested in feedback! | The Madison Math Circle is organized by a group of professors and graduate students from the [http://www.math.wisc.edu Department of Mathematics] at the UW-Madison. If you have any questions, suggestions for topics, or so on, just email the '''organizers''' [mailto:mathcircleorganizers@g-groups.wisc.edu here]. We are always interested in feedback! | ||
<center> | <center> | ||
<gallery widths= | <gallery widths="500" heights="300" mode="packed"> | ||
File:Uri.jpg|[https://www.math.wisc.edu/~andrews/ Prof. Uri Andrews] | File:Uri.jpg|[https://www.math.wisc.edu/~andrews/ Prof. Uri Andrews] | ||
</gallery> | </gallery> | ||
<gallery widths="500" heights="250" mode="packed"> | |||
<gallery widths= | |||
</gallery> | </gallery> | ||
</center> | </center> | ||
==Donations== | ==Donations== | ||
| Line 237: | Line 209: | ||
=Useful Resources= | =Useful Resources= | ||
== Archived Abstracts == | == Archived Abstracts == | ||
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2023-2024 2023 - 2024 Abstracts] | |||
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2022-2023 2022 - 2023 Abstracts] | |||
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2021-2022 2021 - 2022 Abstracts] | |||
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2020-2021 2020 - 2021 Abstracts] | [https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2020-2021 2020 - 2021 Abstracts] | ||
Latest revision as of 15:58, 25 November 2024
For the site in Spanish, visit Math Circle de Madison
What is a Math Circle?
The Madison Math Circle is a weekly series of mathematically based activities aimed at interested middle school and high school students. It is an outreach program organized by the UW Math Department. Our goal is to provide a taste of exciting ideas in math and science. In the past we've had talks about plasma and weather in outer space, video game graphics, and encryption. In the sessions, students (and parents) are often asked to explore problems on their own, with the presenter facilitating a discussion. The talks are independent of one another, so new students are welcome at any point.
The level of the audience varies quite widely, including a mix of middle school and high school students, and the speakers generally address this by considering subjects that will be interesting for a wide range of students.
After each talk we'll have pizza provided by the Mathematics Department, and students will have an opportunity to mingle and chat with the speaker and with other participants, to ask questions about some of the topics that have been discussed, and also about college, careers in science, etc.
The Madison Math Circle was featured in Wisconsin State Journal: check it out!
All right, I want to come!
Our in person talks will be at, Monday at 6pm in 3255 Helen C White Library, during the school year. New students are welcome at any point! There is no fee and the talks are independent of one another. You can just show up any week, but we ask all participants to take a moment to register by following the link below:
Math Circle Registration Form
All of your information is kept private, and is only used by the Madison Math Circle organizer to help run the Circle.
If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus. If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in 3255 Helen C White Library, on the UW-Madison campus, right next to the Memorial Union).
Fall Schedule
| Fall Schedule | |||
|---|---|---|---|
| Date | Location and Room | Speaker | Title |
| Oct 7 | 3255 College Library | Caitlin Davis | How to Cut a Cake (Fairly) |
| Oct 14 | 3255 College Library | Uri Andrews | Math, Philosophy, Psychology, and Artificial Intelligence |
| Oct 21 | 3255 College Library | Sam Craig | Fractal geometry and the problem of measuring coastlines |
| Oct 28 | 3255 College Library | Cancelled | Cancelled |
| Nov 4 | 3255 College Library | Sam Craig | Proofs of the Pythagorean theorem, new and old. |
| Nov 11 | 3255 College Library | Chenxi Wu | Heron’s method for approximating square roots |
| Nov 18 | 3255 College Library | Diego Rojas | Non-Transitive Dice: The Math That Doesn’t Play Fair |
| Nov 25 | 3255 College Library | Kaiyi Huang | A geometric investigation into a space shuttle failure |
| Dec 2 | 3255 College Library | TBA | TBA |
| Dec 9 | 3255 College Library | TBA | TBA |
| Dec 16 | 3255 College Library | TBA | TBA |
Fall Abstracts
Abstract 10/7
| Caitlin Davis |
| Title: How to Cut a Cake (Fairly) |
|
Imagine you and a friend are sharing a cupcake. How can you cut the cupcake so that each of you gets your fair share? If you've ever shared a cupcake (or some other treat) with a friend, you might have an answer! Now what if you're sharing a cake with several friends? Can we use the same strategy to cut the cake fairly? We'll talk about how math can be used to study questions like this. |
Abstract 10/14
| Uri Andrews |
| Title: Math, Philosophy, Psychology, and Artificial Intelligence |
|
People come to understand the truth via a process of arguing. This could be a philosophical debate. This could be an internal dialogue. This could be in a courtroom. This could be deciding with your family where to go for dinner. These are all different forms of argumentation, with different rules for when you are convinced. In a courtroom, you have to be convinced beyond a reasonable doubt, whereas when deciding where to go for dinner, you might just have to look hungriest to win. These processes can be mathematically modeled. Moreover, this is important for the modern goal of teaching a computer how to think and how to understand human reasoning (Artificial Intelligence). |
Abstract 10/21
| Sam Craig |
| Title: Fractal geometry and the problem of measuring coastlines |
|
A fractal is a shape which looks about the same when you look closely as when you look far away. I will show some examples of fractals that arise in math (like the Sierpinski triangle) and in nature (like the coastline of an island) and discuss the difficulties in determining what the length of a fractal means. |
Abstract 11/4
| Sam Craig |
| Title: Proofs of the Pythagorean theorem, new and old. |
|
The Pythagorean theorem has been known for thousands of years and over that time, people have found a number of different ways to prove the theorem. We will talk about a proof given by Pythagoras, a proof by US President Andrew Garfield, and a very recent proof (that you might have heard of in the news) by Calcea Johnson and Ne'Kiya Jackson. |
Abstract 11/11
| Chenxi Wu |
| Title:Heron’s method for approximating square roots. |
|
We will talk about Heron's method for approximating square roots. This will lead us on a journey through approximation methods including Newton's method, through algebraic concepts like the p-adic numbers, and Hensel's Lemma. |
Abstract 11/18
| Diego Rojas |
| Title:Non-Transitive Dice: The Math That Doesn’t Play Fair. |
|
What if I told you there’s a set of dice where winning doesn’t follow the rules you expect? In this talk, we’ll explore the strange and surprising world of non-transitive dice, where the usual logic of “if A is better than B, and B is better than C, then A must be better than C” simply falls apart. Using math, probability, and a little imagination, we’ll uncover why these dice defy intuition and how they challenge our understanding of competition and strategy. Get ready to think about games—and math—in a whole new way! |
Abstract 11/25
| Kaiyi Huang |
| Title:A geometric investigation into a space shuttle failure |
|
We know that a circle has the same width in every direction, but is it the only object that has this property? NASA engineers assumed so, which, together with a string of other mistakes, might have led to the tragic failure of their space shuttle launch. Let’s look further into this problem so that we won’t make the same mistake again! |
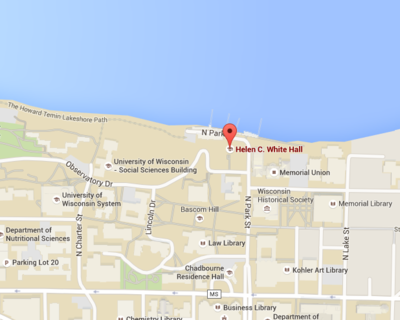
Directions and parking
Our meetings are held on the 3rd floor of Helen C. White Hall in room 3255.
Parking. Parking on campus is rather limited. Here is as list of some options:
- There is a parking garage in the basement of Helen C. White, with an hourly rate. Enter from Park Street.
- A 0.5 mile walk to Helen C. White Hall via these directions, many spots (free starting 4:30pm) in Lot 26 along Observatory Drive.
- A 0.3 mile walk to Helen C. White Hall via these directions, many spots (free starting 4:30pm) in Lot 34.
- A 0.3 mile walk to Helen C. White Hall via these directions, 2 metered spots (25 minute max) in front of Lathrop Hall.
- A 0.2 mile walk to Helen C. White Hall via these directions 6 metered spots (25 minute max) around the loop in front of Chadbourne Hall .
- For more information, see the UW-Madison Parking Info website.
Email list
The best way to keep up to date with the what is going is by signing up for our email list. Please add your email in the form: Join Email List
Contact the organizers
The Madison Math Circle is organized by a group of professors and graduate students from the Department of Mathematics at the UW-Madison. If you have any questions, suggestions for topics, or so on, just email the organizers here. We are always interested in feedback!
Donations
Please consider donating to the Madison Math Circle. Our main costs consist of pizza and occasional supplies for the speakers. So far our costs have been covered by donations from the UW Mathematics Department as well as a generous gifts from private donors. The easiest way to donate is to go to the link:
There are instructions on that page for donating to the Math Department. Be sure and add a Gift Note saying that the donation is intended for the "Madison Math Circle"! The money goes into the Mathematics Department Annual Fund and is routed through the University of Wisconsin Foundation, which is convenient for record-keeping, etc.
Alternately, you can bring a check to one of the Math Circle Meetings. If you write a check, be sure to make it payable to the "WFAA" and add the note "Math Circle Donation" on the check.
Or you can make donations in cash, and we'll give you a receipt.
Help us grow!
If you like Math Circle, please help us continue to grow! Students, parents, and teachers can help by:
- Like our Facebook Page and share our events with others!
- Posting our flyer at schools or anywhere that might have interested students.
- Discussing the Math Circle with students, parents, teachers, administrators, and others.
- Making an announcement about Math Circle at PTO meetings.
- Donating to Math Circle.
Contact the organizers if you have questions or your own ideas about how to help out.
Useful Resources
Archived Abstracts
2015 - 2016 Math Circle Page (Spanish)
Link for presenters (in progress)
Advice For Math Circle Presenters
Sample Talk Ideas/Problems from Tom Davis